Anytime-Valid Neural Uncertainty Quantification for SPECT Imaging

Sat 11 October 2025
Statistics
#uncertainty-quantification, #tomography, #SPECT, #confidence-sequences, #neural-networks, #diffusion-models

Abstract

We develop anytime-valid methods for uncertainty quantification in tomographic imaging, with a focus on single-photon emission tomography (SPECT). In SPECT, sequentially acquired data is used to reconstruct images representing the radioactivity distribution inside the object. In addition to producing image reconstructions, our approach constructs confidence sequences: collections of confidence sets that contain the true but unknown image with high probability simultaneously across all acquisition steps. We investigate two variants: prior likelihood mixing and sequential likelihood mixing. Both employ likelihood-based constructions, but differ in how they use user-defined distributions. We parameterize these distributions using classical statistical estimators (MLE, MAP) as well as neural methods, namely U-Net ensembles and diffusion models. In numerical experiments, we simulate SPECT data and compare the tightness and empirical coverage rate of different confidence sequences. Empirically, sequential likelihood mixing proves to be a particularly effective method for constructing confidence sequences. The performance of this method depends on the image predictor used: U-Net ensembles often yield tight and reliable confidence sets, while in some settings classical estimators (MLE, MAP) perform best. We also present strategies for generating uncertainty visualizations. Our results suggest that combining statistical theory with neural predictors enables principled, real-time uncertainty quantification, which may support clinical decision-making in SPECT and related modalities.

Motivation

In single-photon emission computed tomography (SPECT), we reconstruct a radiotracer activity image from noisy photon counts collected at multiple projection angles. These measurements follow a Poisson process determined by the imaging system, yet standard reconstruction methods—maximum-likelihood, MAP regularization, or neural networks—rarely provide rigorous uncertainty quantification.

Illustration of SPECT Measurements

Illustration of Poisson count measurements \(\mathbf{y} ∼ \mathrm{Pois}(\mathcal{R}(\theta^\ast, x))\) of image \(\theta^\ast \in [0, 1]^{64 \times 64}\) at angles \(x \in \{0, 30\}\).

My thesis investigates how to achieve anytime-valid uncertainty in this setting: uncertainty that remains statistically valid at every stage of data acquisition, not just for a fixed sample size.

Confidence Sequences

The central theoretical tool is a confidence sequence (CS), a time-indexed family of sets

\[ S_1, S_2, \dots \subseteq \Theta \quad\text{such that}\quad \Pr(\forall t:\ \theta^\ast \in S_t) \ge 1 - \alpha. \]

In the above, \(\theta^\ast \in \Theta\) is a unknown parameter living in a known space \(\Theta\) and \(\alpha \in (0, 1)\) is a user-specified error level.

Unlike classical confidence intervals, a CS retains its coverage property across all time steps, that is, for \(\theta^\ast\) is inside all \(S_t\) with a (high) probability of at least \(1-\alpha\). We do not have to worry about multiple-testing. This allows us to continuously monitor uncertainty and decide to stop data collection when a confidence set becomes sufficiently tight.

Theoretical Foundation: Likelihood Mixing

The thesis builds on the Sequential Likelihood Mixing (SLM) and Prior Likelihood Mixing (PLM) theorems developed by Kirschner, Krause, Meziu, and Mojmir (2025). These results provide general constructions of confidence sequences directly from likelihoods.

Prior Likelihood Mixing (PLM) constructs level sets of a marginal likelihood ratio using a fixed prior \(\mu_0\).
Sequential Likelihood Mixing (SLM) generalizes this by updating the prior sequentially into a data-dependent mixing distribution \(\mu_t\).

Crucially, as long as \(\mu_t\) depends only on past data—that is, not on the most recently observed or any future sample—the resulting confidence sequence remains anytime-valid.

Key Findings

Sequential Likelihood Mixing performs best. SLM produced tight, reliable confidence sequences, particularly when combined with U-Net ensembles.
PLM Approximations often under-cover.
Distance-based uncertainty visualizations provide stable, interpretable uncertainty maps that shrink consistently as data accumulate.

Distance-based Uncertainty Visualization — Distance-based uncertainty images across acquisition steps for S-UMix CS.

MLE/MAP baselines perform well at high photon counts but are too inaccurate in low-count settings.

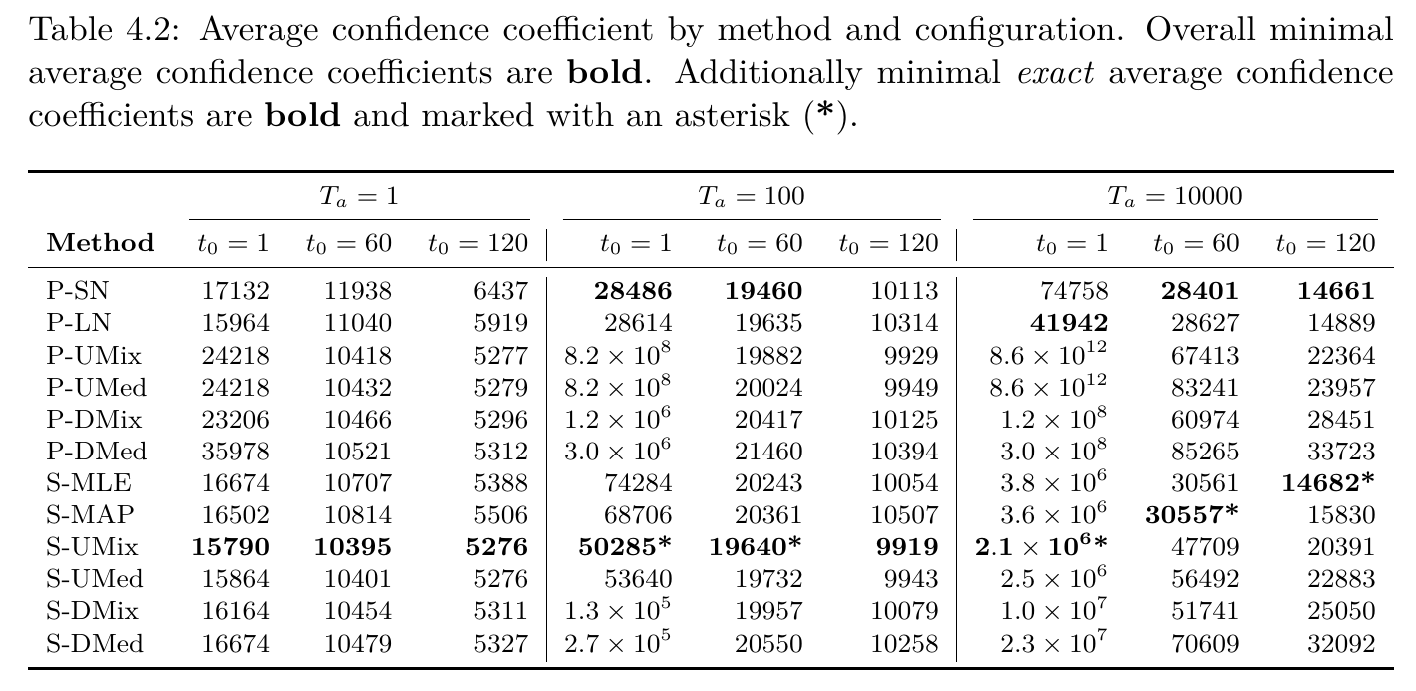
Average Confidence Coefficients

In Table 4.2, lower numbers are better. They represent lower average confidence coefficients and tighter confidence sets. (Check the thesis for a detailed explanation.) The table shows that S-UMix, sequential likelihood mixing using U-Net ensembles, performs best in most settings.

Why It Matters

This work bridges finite-sample statistical guarantees and modern neural image reconstruction. It shows that the likelihood-mixing constructions of Kirschner et al. (2025), can be used to:

deliver real-time, anytime-valid uncertainty in high-dimensional inverse problems,
integrate deep neural predictors with rigorous statistical coverage, and
enable principled stopping criteria based on uncertainty reduction.

In short, the thesis demonstrates that anytime-valid neural uncertainty quantification is feasible for SPECT imaging by pairing theoretically grounded confidence sequences with data-driven approximations.

Resources

Download the thesis (PDF)
Code release (coming soon): MatteoGaetzner/anytime-nuq

This post summarizes my MSc Statistics thesis, supervised by Prof. Dr. Jonas Peters and co-advised by Dr. Johannes Kirschner, conducted within the Swiss Data Science Center (SDSC).